騒音測定時の雑音(暗騒音)はどのように扱い、補正すべきか
騒音測定時の雑音(暗騒音)はどのように扱い、補正すべきか
このページの目次
測定対象以外からの騒音(暗騒音)は必ず存在する
騒音を測定する際、騒音発生源である対象物からのみ騒音が発生していれば雑音の無いピュアな音圧データを測定することが出来ますが、通常そのようなことはあり得ません。人間の耳には全く音が聞こえていないような状況でも、空気の波である音は空気がある以上必ず存在するためです。これは音響を厳密に測定するための「無響室内」ですら同様のことが言え、全く暗騒音(対象物以外による全ての音)が無い状況は通常あり得ないと言えます。つまり、測定対象物から発生する音だけを厳密に測定するのは、一般的に非常に困難です。
複数の騒音が存在すると騒音は互いに干渉し、強めあう
音は空気の波ですので、音源の異なる二つ以上の音は互いに干渉しあいます。つまり、騒音源が複数あると、騒音源が1か所だけの場合と比較して音圧レベル(音の大きさ)は大きくなります。ただし、単純に足せばよい訳ではなく、例えば55dbの音源が二つあると、合成音圧は理論的には58dbとなります(110dBにはなりません)。ちなみに音源の数をもっと増やしていくと、音圧の増加量自体はさらに下がっていきます。
いずれにしても、騒音源が複数ある場合、測定される音圧は複数の音圧を重ね合わせた合成騒音となることに注意が必要です。
暗騒音と測定対象の音圧差が小さいほど影響は大きく、10db以上でほぼ無視できる
一般的に暗騒音の影響は、測定対象との音圧差が10db程度あれば無視できるとされています。これはたとえば、大音量で音楽が流れている中では会話が難しいが、周りが静かな空間だとスムーズに会話が出来るのと同じ仕組みです。周りの音、すなわち暗騒音が大きくなるほど測定対象の騒音を正確に測定するのは難しくなります。したがって本来騒音測定をする場合は十分に暗騒音と測定対象の音圧差が取れる状況で測定をするのが望ましい測定条件です。
暗騒音が無視できない場合は暗騒音補正を行う
暗騒音が無視できない、つまり10db等大きい音圧差が無い場合においては、暗騒音と測定対象両方の騒音を測定し、これらの値を用いて暗騒音補正を行います。暗騒音補正値K1は下記の式で算出することが出来ます
LT(db):(暗騒音を含む)測定対象音圧測定値
LB(db):暗騒音音圧測定値
K1(db):暗騒音補正値
K1=-10*log10(1-10^(-(LT-LB)/10))
この式に従えば、音圧レベル差ΔL=(LT-LB)が7dbの時K1が1.0db、つまり測定対象音圧から1.0dbを引けば、真の測定対象のみの音圧が算出できるというわけです。この式から暗騒音補正値K1と音圧レベル差には下記のような関係があることがわかります。
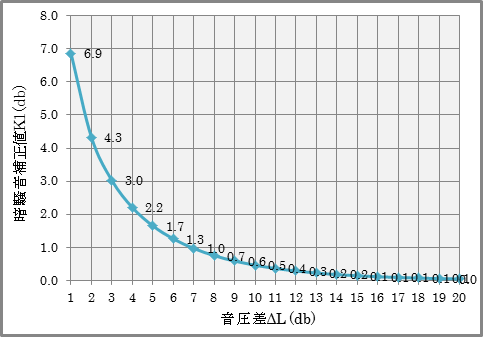
つまり、前述のとおり、音圧レベル差が低いほど、暗騒音の影響が大きいということです。例えばLT=60db、LB=53dbの場合、真の測定対象のみの音圧は59.0dbと算出することが出来ます。ちなみにこれらの補正値は実用級で 6 dB、簡易級で 3 dB以上の音圧差がある場合に適応するべきとされています。
| (暗騒音を含む) 測定対象音圧 LT(db) |
暗騒音音圧 LB(db) |
音圧レベル差 ΔL(db) |
暗騒音補正値 K1(db) |
測定対象のみの 音圧 LT-K1(db) |
| 60 | 59 | 1 | 6.9 | 53.1 |
| 60 | 58 | 2 | 4.3 | 55.7 |
| 60 | 57 | 3 | 3.0 | 57.0 |
| 60 | 56 | 4 | 2.2 | 57.8 |
| 60 | 55 | 5 | 1.7 | 58.3 |
| 60 | 54 | 6 | 1.3 | 58.7 |
| 60 | 53 | 7 | 1.0 | 59.0 |
| 60 | 52 | 8 | 0.7 | 59.3 |
| 60 | 51 | 9 | 0.6 | 59.4 |
| 60 | 50 | 10 | 0.5 | 59.5 |
| 60 | 49 | 11 | 0.4 | 59.6 |
| 60 | 48 | 12 | 0.3 | 59.7 |
| 60 | 47 | 13 | 0.2 | 59.8 |
| 60 | 46 | 14 | 0.2 | 59.8 |
| 60 | 45 | 15 | 0.1 | 59.9 |
| 60 | 44 | 16 | 0.1 | 59.9 |
| 60 | 43 | 17 | 0.1 | 59.9 |
| 60 | 42 | 18 | 0.1 | 59.9 |
| 60 | 41 | 19 | 0.1 | 59.9 |
| 60 | 40 | 20 | 0.0 | 60.0 |
上記補正値を算出した数式のエクセルファイルはこちらからダウンロード可能です。
暗騒音の測定と補正に関するより専門的な知識
騒音問題を正確に把握し、適切な対策を講じるためには、音の大きさ(dB)だけでなく、その性質を多角的に評価する必要があります。以下では、特に重要となるいくつかの専門的な指標や法律について解説します。
-
なぜ単純な引き算ではないのか?デシベルの対数特性とエネルギー和
「測定対象の騒音レベルから、暗騒音のレベルを単純に引き算してはいけないのか?」という疑問を抱く方もいるかもしれません。これは、騒音レベルで用いられるデシベル(dB)が、音のエネルギーを対数で表現した特殊な単位であるためです。デシベルの計算は、足し算や引き算のように単純には行えません。例えば、80dBの音と80dBの音が合わさっても160dBにはならず、約83dBになります。これは、それぞれの音のエネルギーを合計し、それを再びデシベルに変換するという計算が行われるためです。
当ページに掲載されている「暗騒音補正値の表」は、このエネルギー計算に基づいています。測定値(対象騒音+暗騒音)と暗騒音のレベル差から、暗騒音のエネルギー成分を差し引いた結果(対象騒音の真のレベル)を予め計算したものなのです。
-
変動する暗騒音の評価方法(等価騒音レベルLeqの活用)
暗騒音は、常に一定のレベルであるとは限りません。断続的に通過する車の音や、不規則に稼働する隣の工場の機械音など、時間的にレベルが変動する場合も多くあります。このような変動する暗騒音を評価する際に有効なのが「等価騒音レベル(Leq)」です。これは、ある時間内の変動する騒音エネルギーの平均値を、同じエネルギー量の定常音レベルとして表現したものです。
変動の大きい暗騒音を測定する場合は、まず暗騒音そのものを一定時間測定して等価騒音レベル(Leq)を求め、その安定した値を「暗騒音レベル」として採用します。これにより、より信頼性の高い補正が可能となります。
-
周波数分析による、より精密な暗騒音補正
測定対象の騒音と暗騒音の性質が大きく異なる場合、周波数分析を用いることで、より精密な補正が可能です。例えば、測定したい音は高周波成分が主体であるのに対し、暗騒音は低周波の「ブーン」といううなり音であるケースを考えます。この場合、全体の騒音レベル(オーバーオール値)で補正を行うと、本来影響の少ない低周波の暗騒音によって、測定したい高周波成分の評価が不正確になる可能性があります。
そこで、周波数分析器を用いて、測定値(対象騒音+暗騒音)と暗騒音をそれぞれ周波数帯域ごとに測定します。そして、その帯域ごとにレベル差を算出し、補正を行うのです。これにより、特定の周波数帯域にのみ存在する暗騒音の影響を的確に排除し、測定対象の騒音の周波数特性を正確に評価することができます。
-
暗騒音補正の公的規格(JIS Z 8731)
当ページで解説している暗騒音の補正方法は、当社の独自ルールではなく、JIS(日本産業規格)にも定められている公的な手法です。具体的には「JIS Z 8731 環境騒音の表示・測定方法」において、騒音測定時の暗騒音の影響に関する規定があり、その補正方法が明記されています。レベル差が10dBを超える場合は補正不要、3dB未満の場合は測定不能、といった基準はこのJIS規格に基づいています。公的な調査報告書などを作成する際には、この規格に準拠した測定と補正が求められます。
測定対象の正確なデータを得るには
測定対象の正確なデータを得るためには「測定対象による騒音の測定データ」を得た上で
「測定対象による騒音が発生していない状態での暗騒音測定データ」を得て、暗騒音補正を行うべきか否かを吟味する必要があります。そして、必要と判断された場合には補正を行うことで理論上正確な「測定対象のみによる騒音のデータ」が得られる訳です。当社ではこれらの測定データを得るためのサービスを豊富にご用意しております。また、上記のデータを得るための条件の擦り合わせ等ご相談も多数承っておりますので、正確な測定データがご必要の際はお気軽にお問い合わせください(>>お問い合わせはこちらから)。



 騒音測定時の雑音(暗騒音)はどのように扱い、補正すべきか
騒音測定時の雑音(暗騒音)はどのように扱い、補正すべきか